今回の「かずの不思議」は、毎日つかっているカレンダーをあらためて詳しく調べてみると、実は、そこに「エッ?!」と思うような「不思議」が隠れていることを、みんなで協力して発見することでした。
昨年のカレンダー(自分で組立可能なミニのもの)を全員に配ったところ、最初に手を上げて質問したのは、「一ヶ月が30日と31日の2種類あるのは、なぜ?」「2月だけ28日なのは、なぜ?」「4年ごとにうるう年があるのは、なぜ?」という、「カレンダーの秘密」ならぬ「カレンダーの不思議」についての質問でした。これは私の意図に反する予想外の質問でしたが、先ずこれらの質問に関して、ユリウス暦のことを話さなくてはなりませんでした。
次に、今年6月のカレンダーをホワイトボードに貼って、「数の並び方に注目しよう」と呼びかけました。
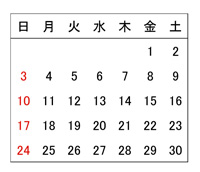
「① よこ方向は、どの行も1ずつ増えている」
「② たて方向は、どの列も7つずつ増えている」
と誰かが言うと、「あ、ほんとうや!」、「①は日が一日ずつ増えるからあたりまえ、でも②はなぜだろう?」、しばらくして「一週間は7日だ!」の声があがりました。
昨年度のカレンダーの全月のたての数字の並びを、みんなに確認してもらったら、「1・8・15・22・29」「2・9・16・23・(30)」「3・10・17・24・(31)」「4・11・18・25」「5・12・19・26」「6・13・20・27」「7・14・21・28」の7種類しかないことが発見できました。そして、その理由は「先の②と、2月以外の一ヶ月は30日か31日であるから」と確認できました。でも、このことが「よく理解できない!」という人もいました。
さて次は、1から9まで 3×3の数の並びをホワイトボードに書き、「一列に並んだ数字を足したときに、なにか不思議なことが起こっていないかな?」と尋ねました。

しかし、なかなか手が上がらないので、ヒント用の問題形式のプリントを配布したら、「最初の行の1・2・3の和は6で、まん中の2の3倍」「次の行の4・5・6の和は15で、まん中の5の3倍」「3行目の7・8・9の和は24で、まん中の8の3倍」になっていることに、ほとんどの人が直ぐに気づきました。
いま調べたことに倣って、元のカレンダーから3×3の数の並びをいくつか取り出し、同じことを調べてもらいました。そうすると、カレンダーの場合も「どの行、どの列の3つの数の和も、まん中の数の3倍になっている」 …③ が確認できました。さらに「斜めの3つの数の和も、まん中の数の3倍だ!」…④ と6年生の一人が叫びました。
実際、最初のカレンダーから、下の図のように3×3の数の並びを取り出すと
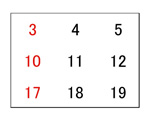
斜めの3・11・19の和は33で、まん中の11の3倍
斜めの5・11・17の和は33で、これもまん中の11の3倍
たての4・11・18の和は33で、これもまん中の11の3倍
よこの10・11・12の和も33で、これもまん中の11の3倍
になっています。
結局「まん中の11を通る たて、よこ、斜め の並びの3つの数の和のいずれもが、まん中の数11の3倍になっている」ことを、みんなで確認しました。でも、3つの数の和を暗算で求めることが苦手な人は、この辺りで授業への集中が途切れそうでした。
続けて、「これらの3×3の9つの数全部の和を、パッと求める方法があるだろうか?」と問うたところ、「ひょっとすると、まん中の9倍になるのとちがう?」…⑤ と、もう一人の6年生が叫びました。
そこで、これまでに分った方法を利用して、9つの数の和を計算してみました。
一行目の和は、3+4+5=4×3 だから12
二行目の和は、10+11+12=11×3 だから33
三行目の和は、17+18+19=18×3 だから54
したがって、全部の和は 12+33+54=99
そして、11×9=99 なので、確かに⑤がなりたっています。
カレンダーがもつ ③、④、⑤の不思議な性質を下図の3×3の9つの数についても確認しようと提案しましたが、4年生だけでなく、6年生も二桁3組の数の和を計算するのを「こんなん面倒くさ過ぎるわ!」とボヤきました。
それで、仕方なく私が全部の和をホワイトボード上で 198 になることを算出して見せて、22×9=198 と一致することを確認しました。(注)
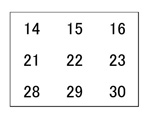
以上が今回の探究学習の主要な流れです。④を推定した6年生と、⑤を推定した6年生はそれぞれ別な発見を授業の終了間際にもってきてくれました。それは次の(イ)と(ロ)です。
(イ)長方形の四隅の数のうち、対角線で結ばれる2組の数の和は、互いに一致する。(例えば6月のカレンダーの場合は、3・16と9・10、5・30と9・26など)
(ロ)隣り合う たての2つの数の和は、2ずつふえる。(例えば6月のカレンダーの場合は、3・10、4・11、5・12、6・13の和は、それぞれ2ずつふえている)
二人はこの現象に気付いただけでなく、なぜそうなるか、その理由も説明することができました。(M.M)
(注)9つの数の和を実際に手計算でやってみることで、不思議な⑤の性質を全員に実感してもらいたかったのですが…。最初から電卓を活用すればよかったと、後で反省しています。